Unsupervised learning

Alexandre Boulch

www.boulch.eu

IOGS - ATSI

     

Introduction

     

What is unsupervised learning?

Definition

Find underlying structures in unlabeled data.

Motivations

  • Most of the data is unlabeled
  • Annotations are expensive
  • Annotations are slow
     

What do we do with unsupervised learning?

Dimension reduction

Keep only useful information: easy storage, computation speed up . . .

Clustering

Group data by similarity. Classification (without a guide)

Visualization

Humans do not deal well with n > 3 dimensional space.

Feature extraction

Pre-train neural network on large data (no label) to be further used on small datasets.

     

Dimension reduction

     

Principal Component Analysis

Draw a fish

  • Fishes are 3D objects
  • How to create 2D representation?
  • Find the best point of view
  • Even better: perspective (Giotto, 1420)
     

Principal Component Analysis

Draw a fish

  • Fishes are 3D objects
     

Principal Component Analysis

Draw a fish

  • Fishes are 3D objects
  • How to create 2D representation?
     

Principal Component Analysis

Draw a fish

  • Fishes are 3D objects
  • How to create 2D representation?
  • Find the best point of view
     

Principal Component Analysis

Draw a fish

  • Fishes are 3D objects
  • How to create 2D representation?
  • Find the best point of view
  • Even better: perspective (Giotto, 1420)
     

Principal Component Analysis

Principal Component Analysis

PCA is a prejection method to represent the data by dimension number reduction.

     

Principal Component Analysis: formalism

Linear algebra

  • a vector space: structure allowing the combination of linear vectors
  • a base: a family of free and generator vectors
     

Principal Component Analysis: formalism

Linear algebra

  • a vector space: structure allowing the combination of linear vectors
  • a base: a family of free and generator vectors
  • Base change: endomorphism ,
     

Principal Component Analysis: formalism

Linear algebra

  • a vector space: structure allowing the combination of linear vectors
  • a base: a family of free and generator vectors
  • Base change: endomorphism ,
  • Projection: linear application of , being a sub-vector space of
     

Principal Component Analysis

PCA geometric objective

PCA search for the sub vector space (with reduced dimensio) for projection which allow the more accurate projection of the data.

     

Principal Component Analysis: formalism

Statistics

Let and be 2 Random Variables

  • Average
  • Variance : dispersion measure
  • Covariance : measures de correlation

Let a random vector:

  • Variance-Covariance matrix

     

Principal Component Analysis

PCA statistical objective

PCA aims at:

  • Dispersion maximization on the first dimensions of the base:
    and
  • Dimensions are not correlated:
     

Principal Component Analysis: algorithm

Samples of a random vector . matrix of s vectors.

  1. Center the sample , s.t.,
  2. Build the variance-covariance matrix

  1. Diagonalize :

  1. Sort the eigenvalues in decreasing order (and eigenvectors)

We obtain the tranfer matrix et the eigenvalues .

symmetric, real, so can be diagonalized (Weirstrass theorem)
     

Principal Component Analysis: properties

  • Transfer matrix made of the vector of the new base:

  • Projection matrix in an optimal sub-vector space:

     

Principal Component Analysis: properties

  • The eigenvectors assotiated with the eigenvalues
    sorted in increasing order
  • Variance statistical information carried by the dimension. Link to signal theory:
    • The principal components (with a large variance) represent the signal
    • Low variance components are the noise
     

Principal Component Analysis: examples

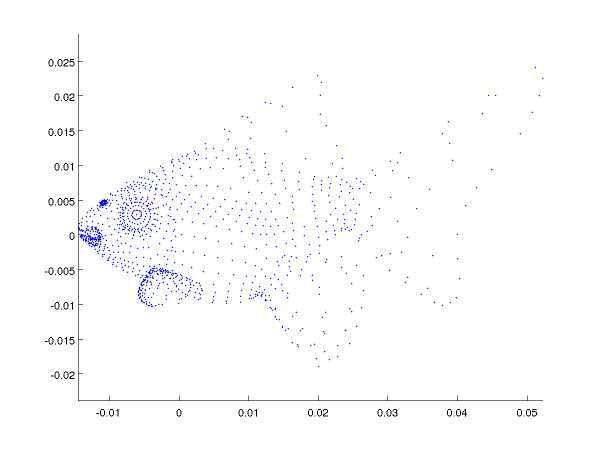
Back to the fishes

Points of on the surface of the Discus Alenquer

Variances:

Eigen vector base:

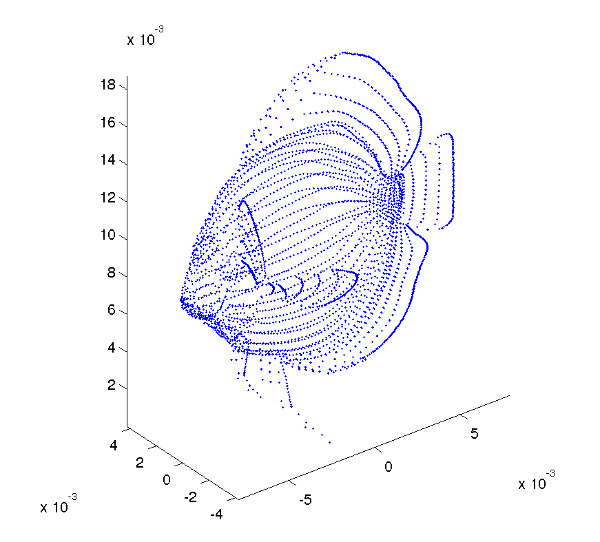
center

     

Principal Component Analysis: examples

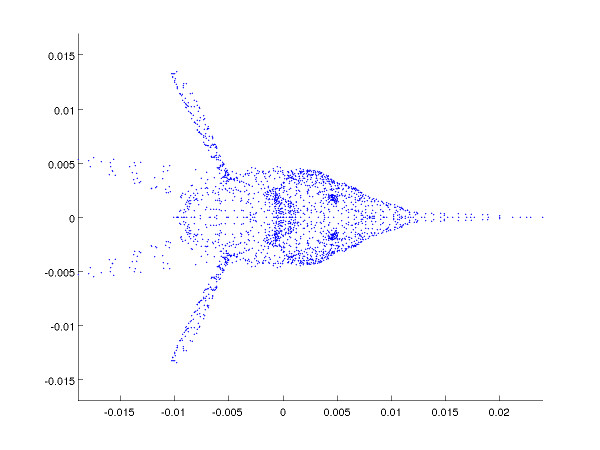
Back to the fishes

Projection on the two first components (or the two last)

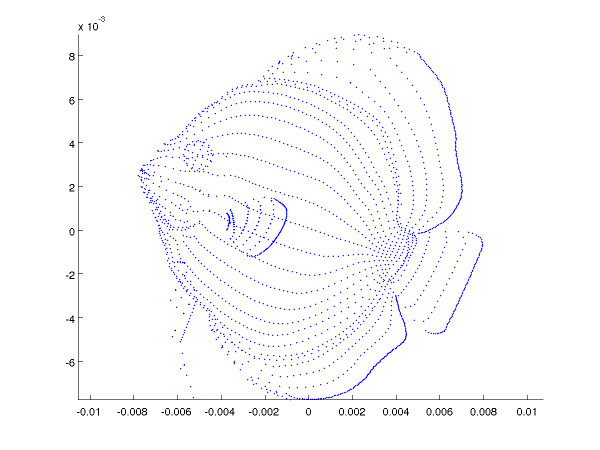
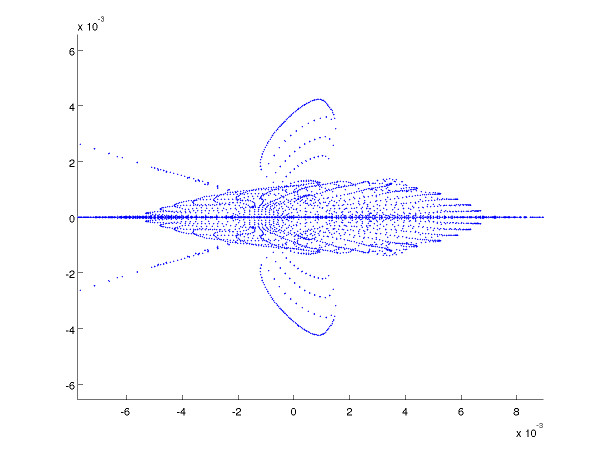
center

center

     

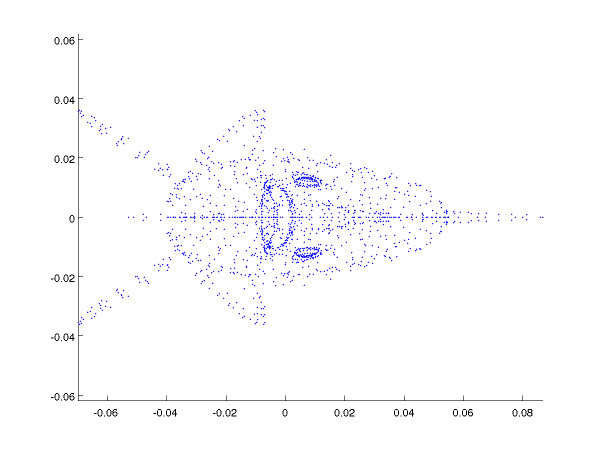
Principal Component Analysis: examples

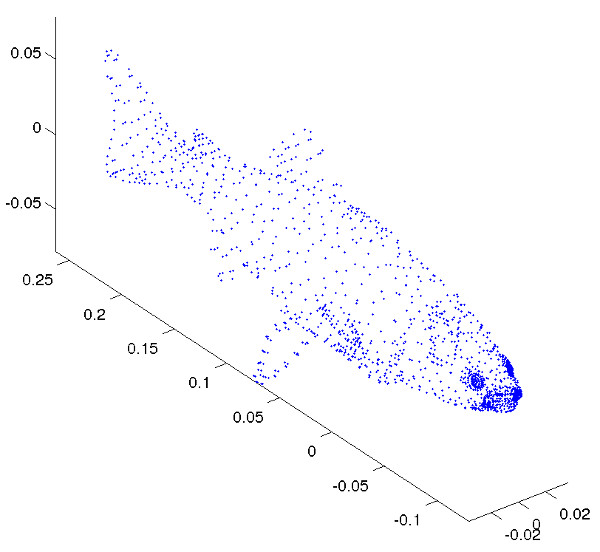
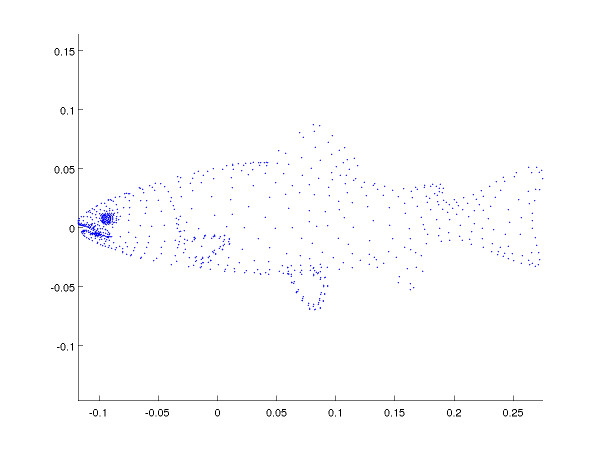
More fishes

3D vs projection on the two first components (canonical representations) and the last.


     

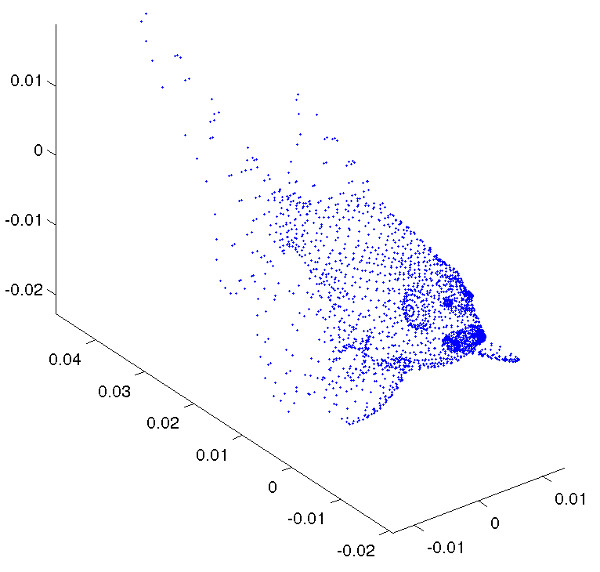
Principal Component Analysis: examples

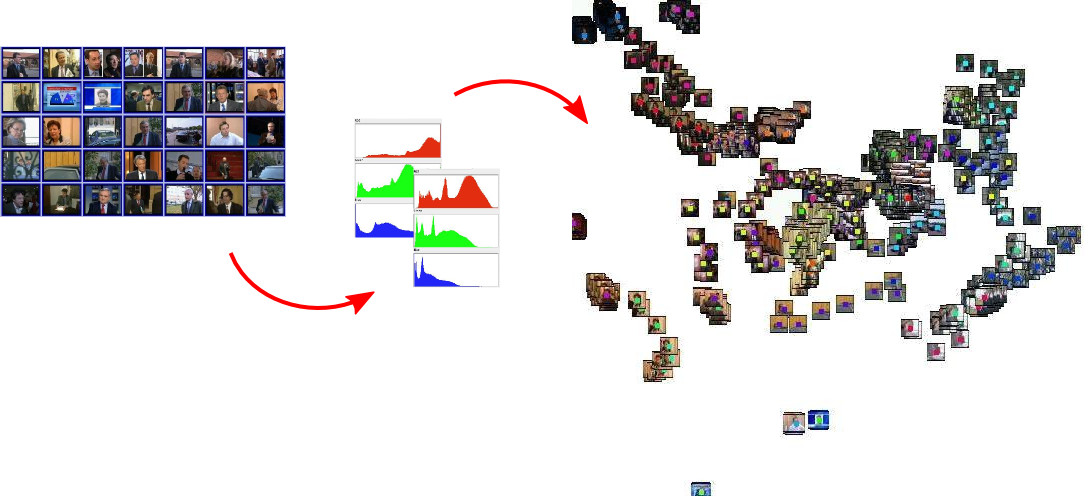
Video analysis

Video images converted to color histrograms and visualized with the 2 first components of the PCA.


center

     

Principal Component Analysis

Key points

  • High dimension data representation
  • Dimension reduction
  • Variable decorrelation
  • Based on data variance-covariance matrix diagonalization

Usage

  • Data preprocessing for data analysis (see the first classes)
  • Visualization
     

Clustering

     

Clustering

Definition

  • Find categories for close/similar objects
  • unsupervised classification of the unlabeled data in

Objectives

  • Group similar data, requires a notion of distance
  • Categorization
     

K-means

  • Let be the cluster number
  • A cluster (indexed by ) is a group of points
  • Let define if belongs to cluster
  • Let be the cluster prototypes (caracterization of a prototype)

K-means

Algorithm minimizes:

     

K-means

Algorithm

Initilize s, and iterate:

  • Assign each to the closest
  • Recompute the s according to:

(average location of the group)

     

K-means

Properties

  • decreases at each iteration
  • There is a fixed number of cluster, so the algorithm converges
  • But the solution may not be optimal (local minimum)

center

Initialization

  • Initialization is important
  • E.g., chose the initial among the data
     

K-means

Statistical variant

  • Parameters of Gaussian Mixture Model (GMM) estimated by the Expectation-Maximization algorithm.
  • is the realisation of a random vector, modeled with a Gaussian mixture:

  • Estimate:
     

K-means

Variants and tricks

  • Fuzzy C-means: , a point can belong to several clusters
  • Different distance: Mahalanobis distance (FCM), complete covariance matrix (GMM)
  • Outliers: if to high,
  • Criteria for estimation
  • estimation: uniformly spread among the data
     

Clustering: other approaches

Partitionnement spectral:

  • Similarity matrix,
  • Dimension reduction (first eigen
    vectors)
  • K-means

complex objects, non vectors

     

Clustering: other approaches

DBSCAN

  • Data partionning in categories of MinPts points in a radiusϵ
  • Going through the data step by step to add in a category

Automatic estimation of the number of categories,
deal with outliers

     

Self-supervised learning

     

Overview

  • Principles
  • Image-based transformations
  • Contrastive approaches
  • SimCLR
     

Self-supervised learning

Objective

Create a good features for a downstream task.

Pre-training of the network

Create a pretext task to train the network on.
The labels for task a generated automatically.

Downstream task

This the real final objective. It could be classification, regression...
It is trained in a supervised manner.

     

Image-based transformation

Key idea

To predict the transformation of an image, you must \textit{understand} what is in the image.


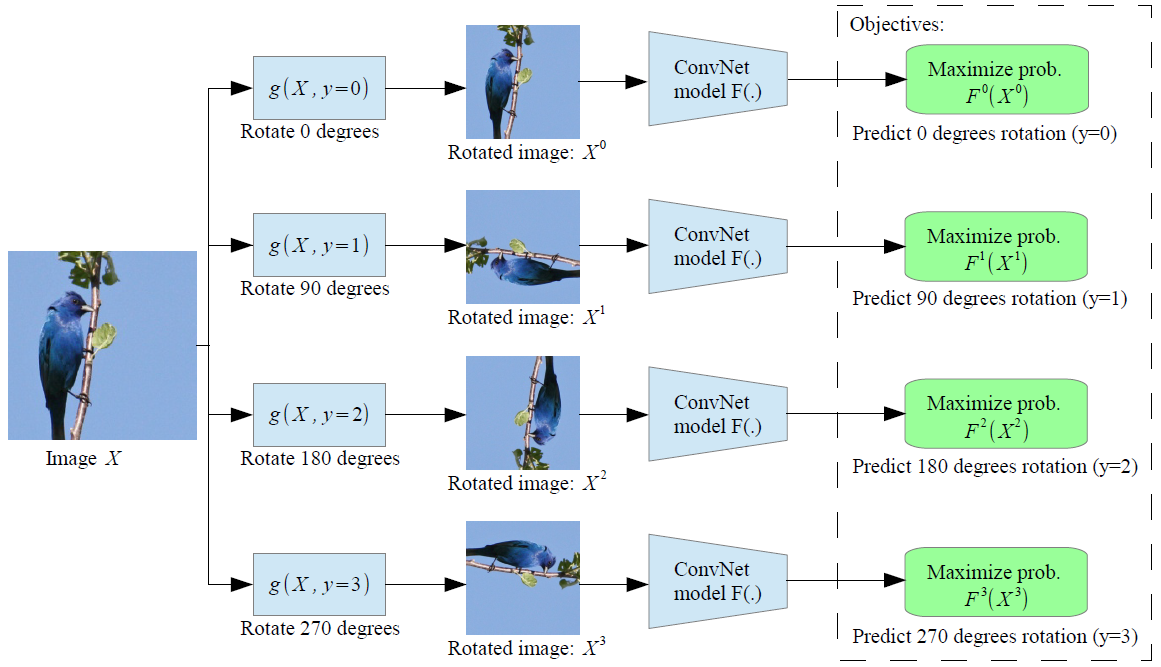
center

     

Image-based transformation: rotation

Transformation

Random rotation of the image.
Four classes: .
Simple classification problem.

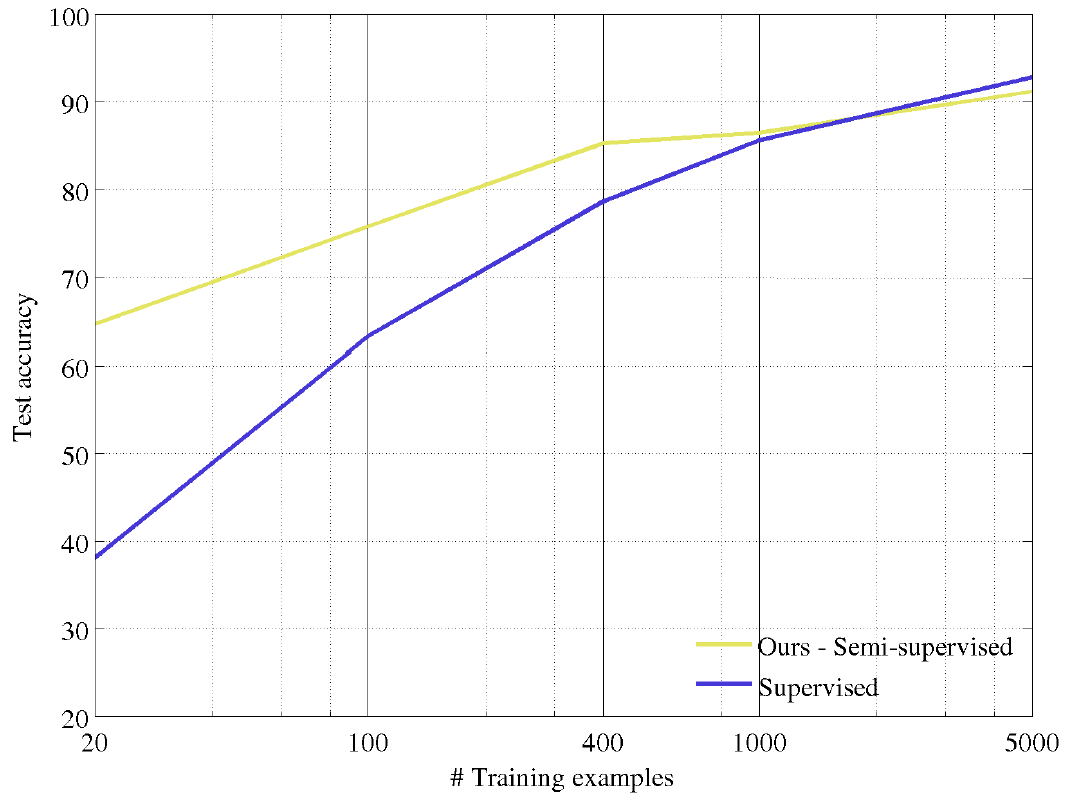
center

     

Image-based transformation: rotation

Transformation

Random rotation of the image.
Four classes: .
Simple classification problem.

Semi-supervised learning

Pre-training: all data (no label)

Target: part of the data with labels

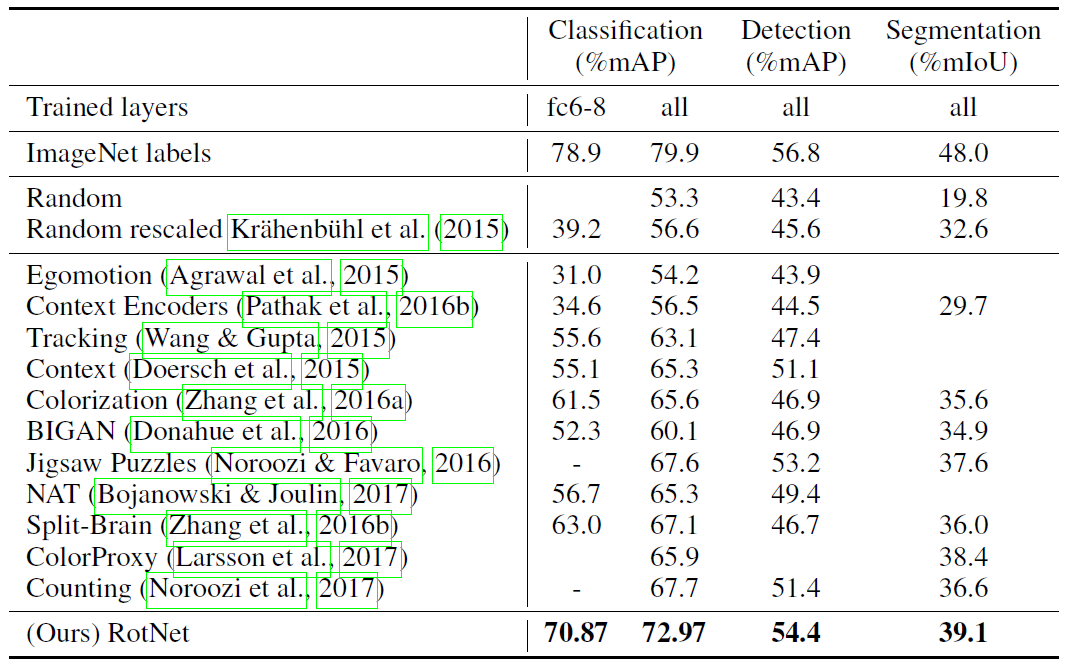
center

     

Image-based transformation: rotation

Transformation

Random rotation of the image.
Four classes: .
Simple classification problem.

Semi-supervised learning

Pre-training: all data (no label)

Target: part of the data with labels

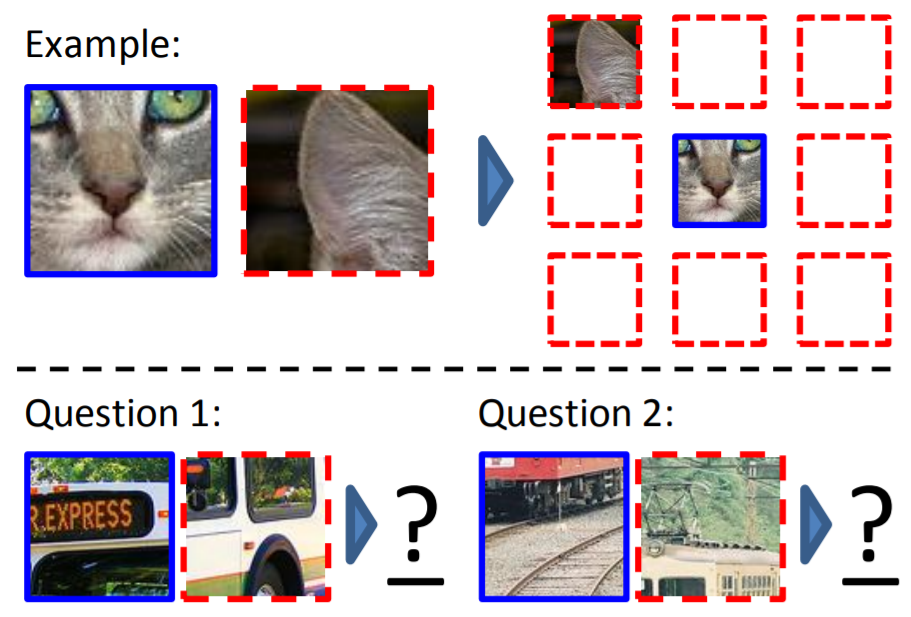
center

     

Image-based transformation: relative position

Transformation

Create a pair of patch, find their relative position.
To solve problem, you need to understand the object.

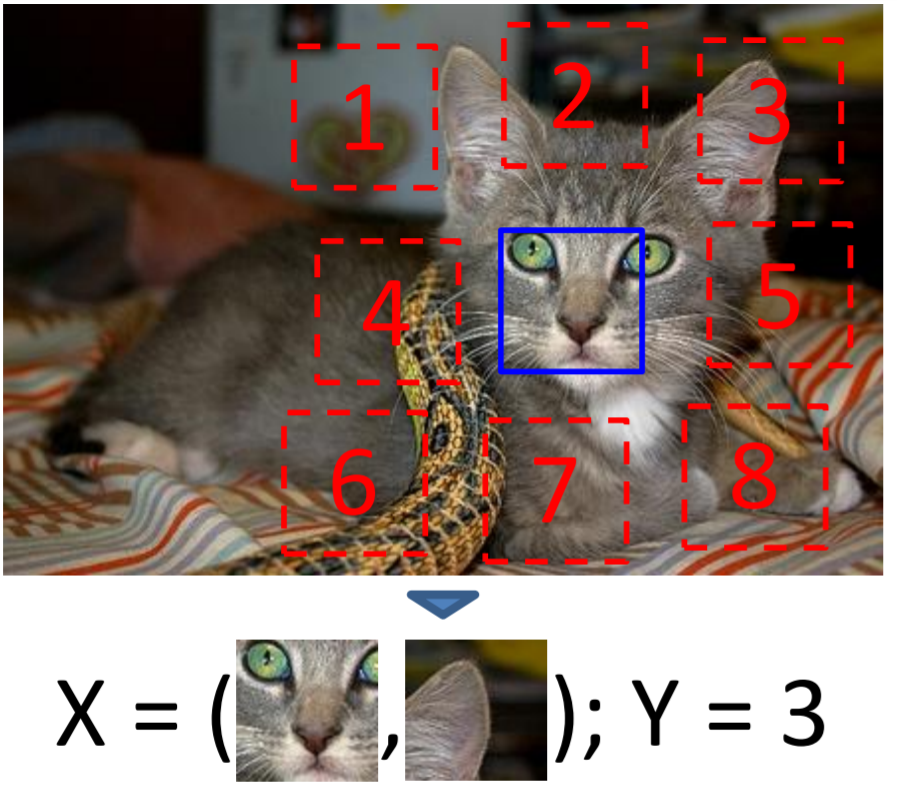
center

     

Image-based transformation: relative position

Transformation

Create a pair of patch, find their relative position.
To solve problem, you need to understand the object.

Problem

Classification with 8 classes

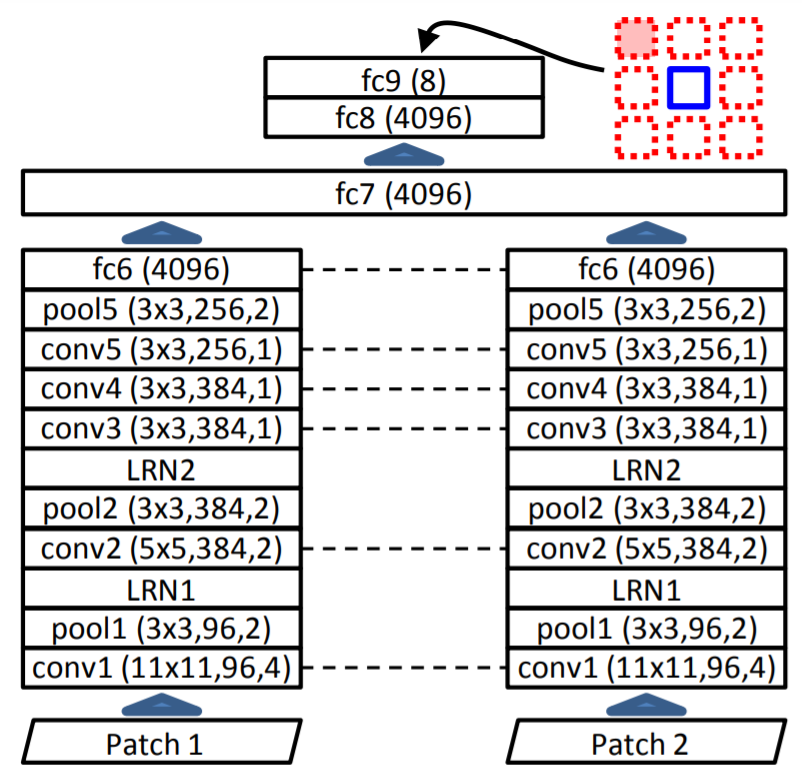
center

     

Image-based transformation: relative position

Transformation

Create a pair of patch, find their relative position.
To solve problem, you need to understand the object.

Problem

Classification with 8 classes

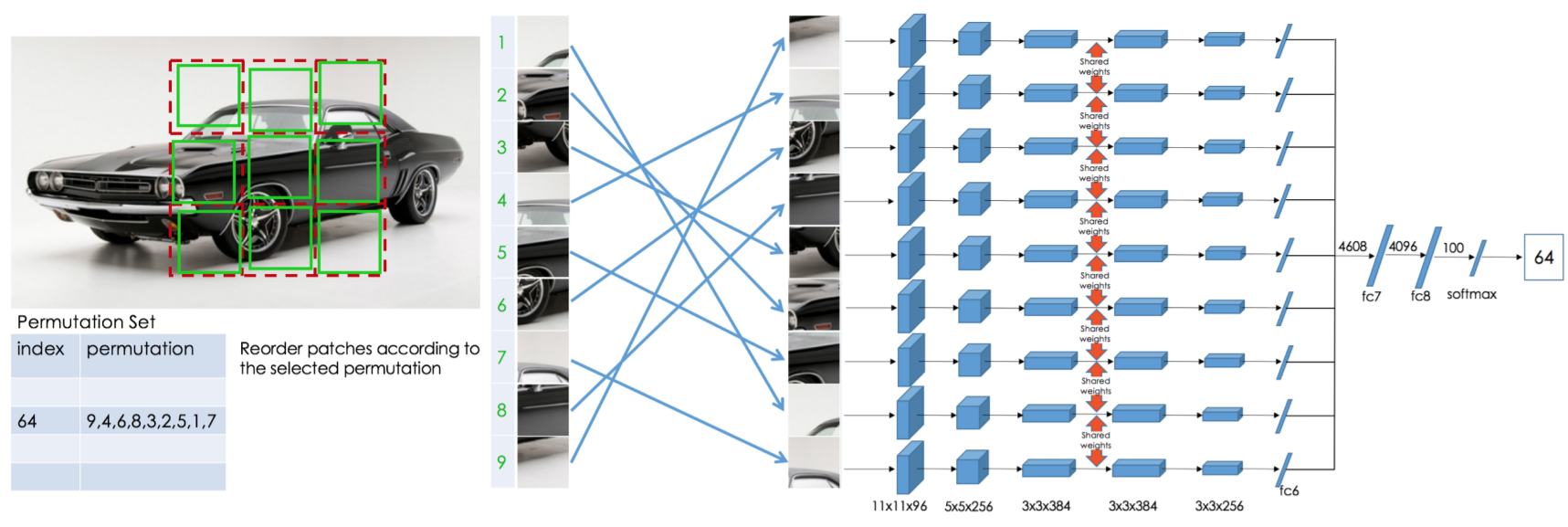
center

     

Image-based transformation: jigsaw puzzle}

center

     

Image-based transformation: jigsaw puzzle}

center

     

Contrastive methods

Image based methods

Predict a transformation of an image.

but may not require a complete knowledge of the object.

What properties the pre-trained network should have ?

  • robust to image variation (illumination, deformation)
    Produce identical features for the same object
  • disciminative with respect to different objects
    Produce different features for different objects
     

SimCLR

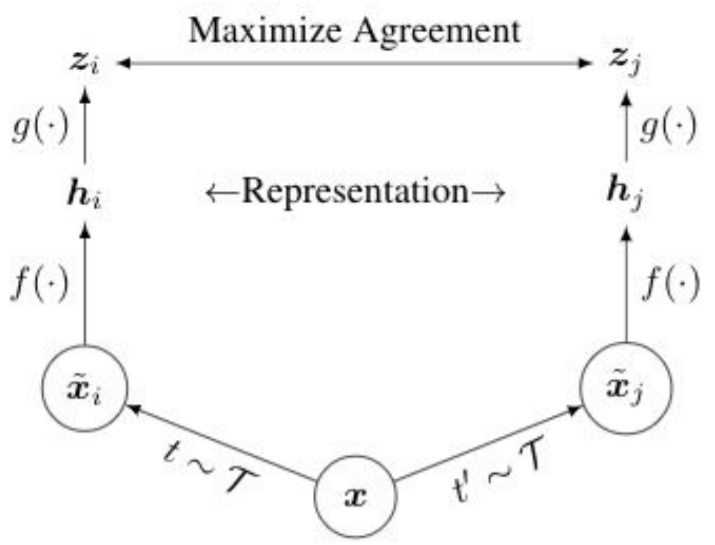
center

     

SimCLR

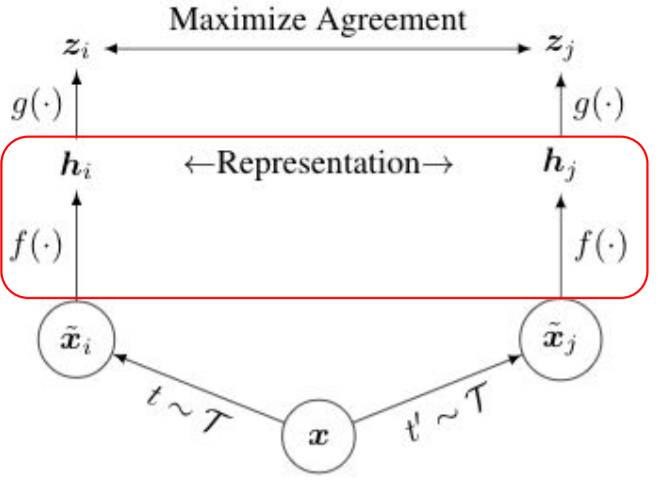
center

     

SimCLR

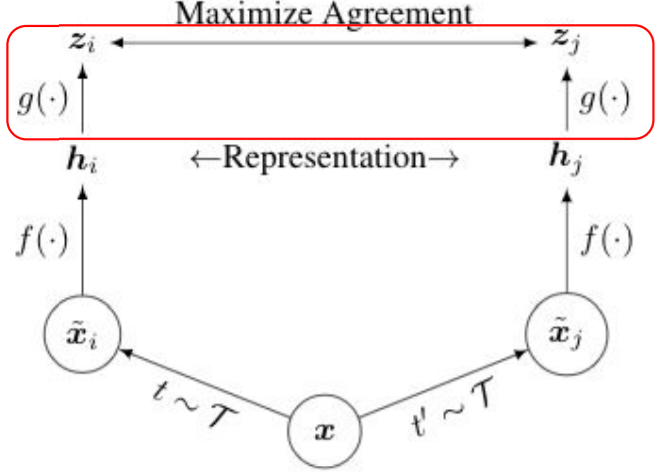
center

     

SimCLR

center

     

SimCLR

center

     

SimCL

center

     

Loss function

Let

The loss function is:

Analysis

A cross entropy applied label corresponding to the pair generated from .

     

Conclusion

Unsupervised learning is one of the big thing in machine learning now.
• Can we extract better/general features?
• Can we reduce the training time?
• Do we really exploit all the information in the data?

Neural Network notes